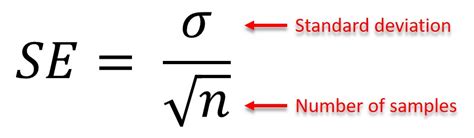-
Tabla de contenido
¿Qué es el error estándar?
El error estándar es una medida de la variabilidad de una estimación estadística. Se utiliza para indicar cuánto puede variar una estimación de una muestra a otra. En otras palabras, el error estándar nos dice cuánto confianza podemos tener en la precisión de una estimación.
¿Cómo se calcula el error estándar?
El error estándar se calcula dividiendo la desviación estándar de una muestra por la raíz cuadrada del tamaño de la muestra. Matemáticamente, se expresa de la siguiente manera:
error estándar = desviación estándar / √n
Donde la desviación estándar es una medida de la dispersión de los datos en la muestra y n es el tamaño de la muestra.
Importancia del error estándar
El error estándar es una medida crucial en estadística, ya que nos permite evaluar la precisión de nuestras estimaciones. Cuanto menor sea el error estándar, mayor será la precisión de la estimación. Por lo tanto, es importante tener en cuenta el error estándar al interpretar los resultados de un estudio o experimento.
Intervalos de confianza
El error estándar también se utiliza para calcular intervalos de confianza, que son rangos dentro de los cuales es probable que se encuentre el verdadero valor de la población. Cuanto más estrecho sea el intervalo de confianza, mayor será la precisión de la estimación.
Comparación de estimaciones
Al comparar dos estimaciones, es importante tener en cuenta el error estándar de cada una. Si las estimaciones tienen errores estándar similares, es más probable que sean comparables. Por otro lado, si las estimaciones tienen errores estándar muy diferentes, es posible que una sea más confiable que la otra.
Conclusiones
En resumen, el error estándar es una medida de la variabilidad de una estimación estadística. Se calcula dividiendo la desviación estándar de una muestra por la raíz cuadrada del tamaño de la muestra. El error estándar es importante para evaluar la precisión de las estimaciones, calcular intervalos de confianza y comparar estimaciones. Por lo tanto, es fundamental tener en cuenta el error estándar al interpretar los resultados de un estudio o experimento.